What Is Electric Flux
Electric flux is a physics term used to explain electric fields passing through a surface. Flux is a flow, and it quantifies flow, or the amount of flow, of an electric field through a surface. You can imagine it as the number of electric field lines that flow through an area.
It is a central topic in electrostatics and the basis of learning electric fields, charges, and Gauss’s law.
Electric flux has some important uses in scientific and engineering applications such as electronics, electromagnetism, and electric circuit theory.
In short, electric flux provides an idea of how much at what rate electric field lines are emerging from a surface.
Symbol for Electric Flux
Electric flux is represented by the Greek symbol Φ (Phi), and its unit of measurement in SI is volt meter (V·m).
It can therefore be expressed as:
Symbol for electric flux: ΦE or Φ
It is described by:
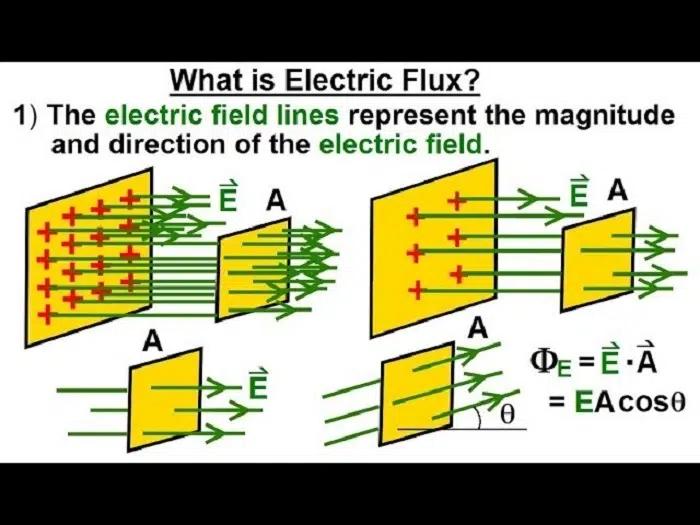
Φ = E × A × cosθ
where:
Φ = electric flux
E = electric field strength
A = area through which the field lines are passing
θ (theta) = angle between electric field and normal of the area
The equation is a measure of the rate of electric field passing into an area.
Understanding the Electric Flux
Imagine electric field lines as arrows indicating the direction of electric force around a charge. When there are plenty of arrows cutting through a surface, the electric flux is huge. When none or few of the lines are cutting through, then the flux is very small.
When the field is perpendicular to the surface, the flux is largest.
When the field is parallel to the surface, the flux is zero.
This means angle θ, has a significant impact on total flux.
If θ = 0° → cos(0) = 1, therefore the flux is maximum.
If θ = 90° → cos(90) = 0, therefore the flux is minimum.
This shows electric flux depends on field strength and field lines direction to the surface.
Equation of Electric Flux
Electric flux via a surface is quantitatively represented as:
Φ = E × A × cosθ
For a uniform or plane electric field, an infinitesimal flux dΦ through an infinitesimal area dA is:
ndΦ = E · dA
And for the entire surface:
Φ = ∫ E · dA
We sum up all the infinitesimal electric field strengths on the surface to obtain total electric flux.
Where It Comes From
The equation is a result of vector math. The dot product (·) in E · A tells us we’re extracting the component of the electric field perpendicular to the surface.
Flux is thus a function of cosθ because it’s a measure of the amount of field going straight through the surface.
Electric Flux and Gauss’s Law
Gauss’s Law, the easiest of the laws of electromagnetism, is applied directly to electric flux.
It simply says that the total electric flux through a closed surface is equal to the charge enclosed divided by the free space permittivity (ε₀).
Mathematically
Φ = Q / ε₀
where:
Φ = total electric flux
Q = net enclosed charge
ε₀ = free space permittivity = 8.85 × 10⁻¹² C²/N·m²
This legislation permits us to determine electric fields for any type of charge collection such as spheres, cylinders, or planes.
Unit of Electric Flux
SI unit of electric flux is volt meter (V·m) or newton meter² per coulomb (N·m²/C).
Simply:
Because
E = F/q = N/C,
and
A = m²,
then
Flux Φ = E × A = N·m²/C
So, electric flux is in terms that either of these can be expressed.
Positive and Negative Electric Flux
Electric flux can either be positive or negative depending on whether the electric field lines are outward or inward from the surface.
Positive flux: Electric field lines that move through the surface in the outward direction.
Negative flux: Electric field lines that move through the surface in the inward direction.
This distinction is particularly significant in Gauss’s Law for closed surfaces when using it to find the enclosed net charge by the surface.
Electric Flux Through Different Surfaces
Let us observe the electric flux through various surfaces.
- Flat Surface
In case of a flat surface ideally at right angles to a uniform electric field:
Φ = E × A
Every line of force goes straight through, thus maximum flux.
- Flat Surface at an Angle
If the surface is tilted at angle θ with respect to the electric field,
Φ = E × A × cosθ
Flux with increase in angle.
- Closed Surface
For a closed surface like a cube or a sphere, net flux will depend on whether you are getting entering or exiting electric lines of force.
Gauss’s law:
Total flux = 0 if you are getting no enclosed charge.
Total flux = Q / ε₀ if you are getting an enclosed charge.
- Nonuniform or Curved Surfaces
You have your little pieces dA and integrate for total flux:
Φ = ∫ E · dA
You’ll be applying it to more complicated physics problems.
Electric Flux Calculation Example
Let’s take an example.
You have an electric field of 200 N/C over a surface area of 2 m² with the electric field at an angle of 30° from the surface normal.
Then,
Φ = E × A × cosθ
Φ = 200 × 2 × cos30°
Φ = 400 × 0.866
Φ = 346.4 N·m²/C
The electric flux through that surface is approximately 346.4 N·m²/C.
Also Read: Divide Symbol on Keyboard: What Does it Say, How to Perform It, and How to Type It Easy
Conditions That Influence Electric Flux
Electric flux value is based on:
Electric field strength (E) – Stronger field means stronger flux.
Surface area (A) – Larger surface area means stronger field lines going through.
Angle (θ) – It determines the amount of field passing perpendicularly through the surface.
Physical Significance of Electric Flux
Electric flux is a useful tool for visualizing and measuring the interaction between space and charge with an electric field. It gives the concept of the strength of a field in a volume and the manner it is near charges.
Points to note:
It measures the amount of electric lines of force that go through a surface.
It visualizes the interaction of electric field and charge.
It is the foundation of Gauss’s Law and the rest of the electrostatic laws.
It unites electric charge and geometry in physics.
Applications of Electric Flux in Daily Life
Electric flux is not a concept that exists solely in theory, however, and extends to all areas of daily life and technology:
Capacitors: Enables us to learn how electric fields react to dielectric material.
Insulation design: Insulators are created in a way such that the leakage of electric flux is minimized.
Electric shielding: Used in cables and devices to control exposure to electric fields.
Physics and education: Used to illustrate the strength of a field and charge distribution.
FAQs
Q: What symbol is used for electric flux?
A: Electric flux is represented by the Greek letter Φ (Phi).
Q: How is electric flux calculated?
A: Φ = E × A × cosθ.
Q: What is the SI unit of electric flux?
A: N·m²/C or V·m.
Q: Is electric flux negative?
A: Yes. When electric field lines are inward through a surface.
Q: How is electric flux related to charge?
A: Φ = Q / ε₀, where Q is the enclosed charge, by Gauss’s law.
Q: What if the electric field is parallel to a surface?
A: Zero, as no field lines are perpendicular to the surface.
The character of electric flux (Φ) is a rich, solid physics concept. The concept holds electric fields, surfaces, and charges into one comprehensive picture. Electric flux enables us to observe how charges produce fields and how fields interact with bodies within space.
Although I’m certain it may appear to be complex, the concepts are straightforward: electric flux is one way of measuring the “flow” that will be caused by an electric field across an area. You’re memorizing one of the most basic rules of electromagnetism and electrostatics here.
Electric flux is the basis of the engineering of charge and energy going around us, from physics to electrical system design to electronics component engineering.